İkili (binary), onlu (decimal), on altılı (hexadecimal) sayı sistemleri adli bilişim analizlerinde ve veri kurtarma aşamalarında büyük bir önem arz etmektedir. Bu makalemizde sayı sistemlerini detaylı bir şekilde sizlere aktarmaya çalışacağız.
2’lik sayı sistemi (binary): Verilerin anlamlı hale getirilmesi için gereken 1-0 ları bize sunar. Rakamlar 1 ve 0 dır. Basamaklar ikinin kuvveti şeklinde değerlendirilir. Farklı tabanların kullanıldığı ortamlarda belirsizliği önlemek için sayıların sağ alt köşesine tabanları eklenir.
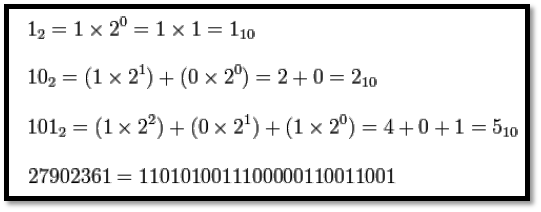
10’lu sayı sistemi (decimal): Normal olarak, günlük hayatta kullandığımız sistemdir. Onlu sayı sistemini ikili sayı sistemine çevirecek olursak eğer;
(275)10 = (?)2
1. 275 / 2 = bölüm :136 kalan =1
2. 136 / 2 = bölüm :57 kalan =0
3. 57 / 2 = bölüm :27 kalan =1
4. 27 / 2 = bölüm :13 kalan =1
5. 13 / 2 = bölüm :5 kalan =1
6. 5 / 2 = bölüm :2 kalan =1
7. 2 / 2 = bölüm :1 kalan =0
8. 1 / 2 = bölüm :0 kalan =1
Bölüm sıfır olana kadar bu işlemi yaparız ve kalanları aşağıdan yukarıya doğru başlayarak yazarız ve sayımız ortaya çıkmış olur.
(275)10 = (10111101)2
16’lı sayı sistemi (hexadecimal): (Hex) bilgisayar belleğindeki 8 bitlik baytları göstermek için kullanılan kestirme bir yoldur. Bu sayı sistemine "16 tabanlı sayı sistemi" denilmesinin nedeni, 16 tane sembolden oluşmasıdır. Sembollerden 10 tanesi rakamlarla (0, 1, 2, 3, 4, 5, 6, 7, 8, 9), geri kalan 6 tanesi harflerle (A=10, B=11, C=12, D=13, E=14, F=15) temsil edilir.
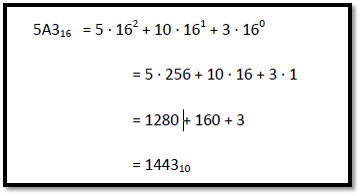
Son olarak binaryden hexadecimal sayı sistemine çevirmeyi görelim:
(110100011)2=(?)16
Burada yukardaki sayıyı sağdan başlayarak 4’er 4’er ayırıyoruz:
(1 1010 0011)=(0001) (1010) (0011) En solda kalan 1’in yanına sıfırları eklememizin nedeni, sadece 4'lü grup haline getirmek içindir. Sayının değerini etkilemez.

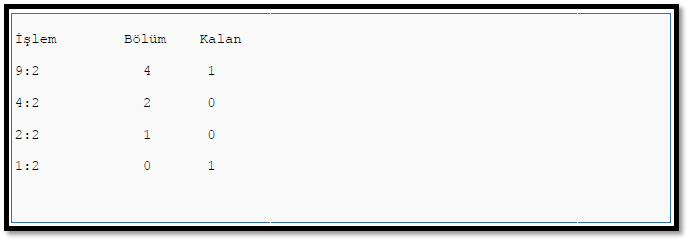
Herhangi bir tabanda verilen sayının başka bir tabanda yazılmasını birkaç örnekle gösterelim. Herhangi bir tabanda verilen sayı önce 10 tabanına çevrilir. Bulunan değer istenen tabana dönüştürülür. Onluk sayının ikili sayıya çevrilmesi: Onluk sayı ikili sayıya çevrilirken İkili sayının tabanı olan 2'ye bölünür. 9 Desimal sayısını İkili sayıya çevirelim. Tablodan görüldüğü gibi 9 sayısı 2'ye bölünür. Bu işlem bölüm sıfır olana kadar devam eder. Kalan kutusundaki rakamlar aşağıdan yukarı doğru alınarak yan yana yazılır.
Sonuç: (9)10 = (1001)2
İkili sayının onluk sayıya çevrilmesi: (101)2 İkili sayısını desimal sayıya çevirelim.
1 x 2 ² + 0 x 2 ¹ + 1 x 2 º => 1 x 4 + 0 x 2 + 1 x 1 = 4 + 0 + 1 = (5)10 bulunur.
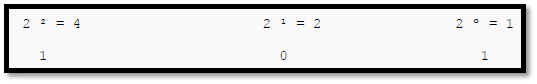
İkili sayının oktal (sekizli) sayıya Çevrilmesi: (11001111011101)2 sayısını sekizli sayı sistemine dönüştürelim. Sekizli sayı sistemine çevirmek istediğimizde bu sefer üçerli kümelere ayırmak gerekmektedir ve eksik bitleri tamamladıktan sonra;

Her bir kümenin temsil ettiği sekizli sayı yazılırsa (11001111011101)2 = (31735)8 eşitliği elde edilir.
İkili sayının heksadesimal sayıya Çevrilmesi: (11001111011101)2 sayısını on altılı sayı sistemine dönüştürelim. Dörderli kümelere ayırma ve eksik bitleri tamamlama sonucunda,
Her bir kümenin temsil ettiği on altılı sayı yazılırsa (11001111011101)2 = (33DD)16 eşitliği elde edilir.

Her bir kümenin temsil ettiği on altılı sayı yazılırsa (11001111011101)2 = (33DD)16 eşitliği elde edilir.
Desimal sayının oktal sayıya çevrilmesi: Desimal sayı oktal sayıya çevrilirken oktal sayının tabanı olan 8'e bölünür. (84)10 desimal sayısını oktal sayıya çevirelim.
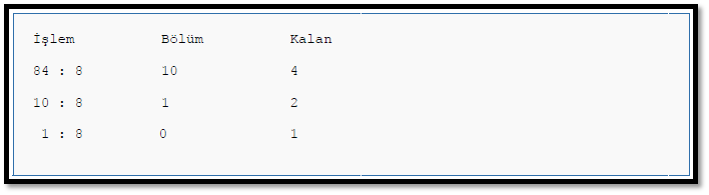
Tabloda görüldüğü gibi 84 sayısı 8'e bölünür. Daha sonra bölüm kutusundaki sayı tekrar 8'e bölünür. (Bölüm sıfır olana kadar). Kalan kutusundaki sayılar aşağıdan yukarı doğru alınarak yan yana yazılır. Çıkan sayı oktal sayıdır.
Sonuç: (84)10 = (124)8
Heksadesimal sayının desimal sayıya çevrilmesi: (4F8)16 sayısını desimal sayıya çevirelim.
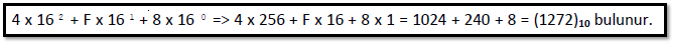
Heksadesimal sayılarla hesap yapılırken harf olarak belirtilen sayıların rakama çevrilerek hesap yapılması daha kolay olacaktır. Örneğin (C = 12 , A = 10 , F = 15) gibi.

Yazar: Öğr. Gör. Dr. Baki NAKKAŞ (Adli Bilişim Uzmanı)




